こんにちは、Educational Enhancementです。

前回のブログでは、「比較」と「相関」という2つの視点が、探究発表の説得力を大きく高めるとお伝えしました。

✅ 比較：グループの違いを示す
✅ 相関：2つの要素の関係性を読み取る

今回はその続編！
「データは取ったけど、どう分析すればいいの？」という人のために、エクセルだけでできる簡単な統計分析のやり方を紹介します。

【ステップ1】平均を出してみよう

使う場面： グループごとの傾向を見たい、比較したいとき

例）AグループとBグループの満足度の点数：

グループ	満足度の点数（例）
A	7, 8, 8, 9, 8
B	2, 5, 8, 11, 14

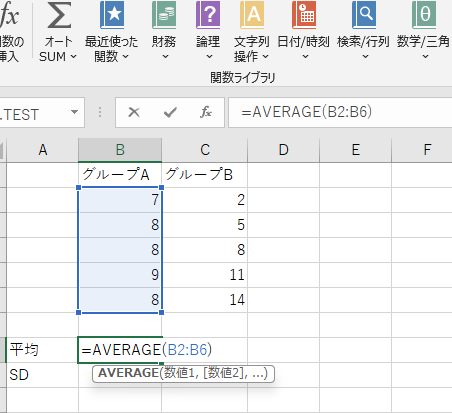
エクセル関数：
=AVERAGE(セル範囲)

たとえば、=AVERAGE(B2:B6)とすれば、B列の平均が出ます。

これで終わりではなく、次に「グループごとの傾向」を探ってみたい。

【ステップ2】標準偏差でバラつきを知る

使う場面： データのばらつきが大きいか、小さいかを知りたいとき

たとえば、2つのグループが同じ「平均8点」だったとしても…

• グループA：7, 8, 8, 9, 8
• グループB：2, 5, 8, 11, 14

どちらも平均は8点ですが、印象はまったく違いますよね？
ここで使えるのが「標準偏差」です。

標準偏差とは、データが「平均からどのくらいズレているか（散らばっているか）」を示す数値です。（実際の探究では、各グループサンプル数が5，というのは少なすぎます。各グループ20以上のサンプルデータがあるといいです。）

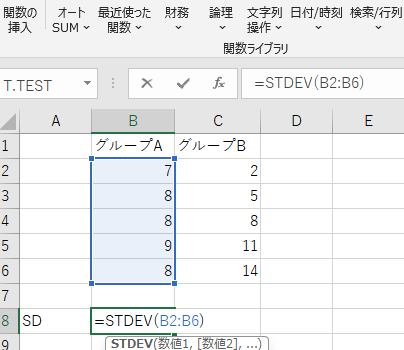
エクセル関数：
=STDEV(セル範囲) ※この関数はSTDEV.Sのこと。探究学習ではサンプルの一部（母集団全体ではないことが多い）のでこれでOK。

• 標準偏差が小さい → 点数が平均に近く、そろっている（ばらつきが小さい）
• 標準偏差が大きい → 点数がバラバラで、個人差が大きい（ばらつきが大きい）

💡 「平均点」だけでは見えない、“データの性格”がわかるのが標準偏差の役割です。

📝 探究レポートでの書き方サンプル（知見の表現）

■ 結果（事実）

AグループとBグループの平均点はともに8.0点であり、一見すると両者に差はないように見える。しかし、**標準偏差（SD）**に注目すると、以下のような違いがあった。

• AグループのSD：約0.70
• BグループのSD：約4.74

■ 考察（意味づけ）

この結果から、Bグループの方が点数のばらつきが大きく、個人差がかなり大きいことがわかる。一方で、Aグループの点数は平均に近く、意見や満足度が安定していると考えられる。

👉実際の詳しい使い方は、このサイトがベスト！　※左をクリックしよう

【ステップ3】相関係数で関係性をチェック！

使う場面： 2つの変数がどれくらい関係しているかを知りたいとき

例）勉強時間と進路満足度の関係：

人	勉強時間（時間）	進路満足度（点）
1	2.0	5
2	3.5	6
3	4.0	7

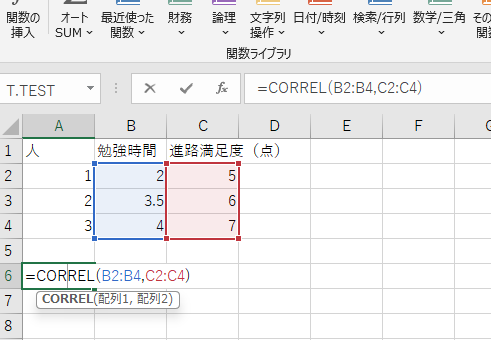
エクセル関数：
=CORREL(B2:B4, C2:C4)　B(勉強時間）　C（進路満足度）

※実際は20以上のサンプルデータがほしいです。

相関係数の目安：
+1.0 → 完全に正の相関
0.0 → 関係なし
−1.0 → 完全に負の相関

🔍 探究レポートでの書き方サンプル（知見の表現）

📘 レポートでの注意点（＋α）

• データ数が少ない（3人）ため、傾向は見えるが一般化には注意が必要。
• 今後は人数を増やし、より信頼性の高い相関分析を行いたい。
• 相関係数は因果関係を示すものではない。

まとめ

統計は「難しそう」に見えて、実は探究学習の強い味方です。

✅ 平均 → グループの傾向が見える
✅ 標準偏差 → ばらつきがわかる
✅ 相関係数 → 要素の関係が見える

これらをエクセルでサクッと使いこなせば、あなたの探究発表は**“なんとなく”から“論拠ある主張”へ**とレベルアップします。

＼ まずは平均とグラフから始めてみましょう！ ／

🔔 次回予告

主観アンケートでもここまでできる！
高校生でもできる、探究調査の設計＆質問づくりのコツを紹介予定です。
「何を聞いたらいいのかわからない…」という人にこそ読んでほしい！

🔁 前回のブログはこちら

👉 比較と相関で、総合型入試に勝つ！
探究発表を“なんとなく”で終わらせない。
「比較」と「相関」の視点で、データに裏づけられた主張へとレベルアップする方法を紹介しています！